电子仓鼠
0%

「鸢尾花书」Python

发表于 更新于 分类于

目标：

  • 机器学习
    • Numpy
    • Pandas
    • Scikit-learn
    • SciPy(数学库)
    • TensorFlow
    • Streamlit 做应用 App
    • NLTK 和 Spacy（自然语言处理）
  • 深度学习
    • PyTorch
    • TensorFlow
  • 数据处理分析
    • 爬虫
  • 可视化
    • Matlibplot
    • Seaborn
  • 视觉
    • OpenCV
  • Python 数学动画工具 manim

image-20240229222111526

Matlibplot和Seaborn的区别：

  • Matplotlib 最基础和最强大的绘图库，灵活性高，学习曲线大，高度定制。
  • Seaborn 基于 Matplotlib 的统计绘图库，美观，快速并容易

二元高斯分布 (bivariate Gaussian distribution)

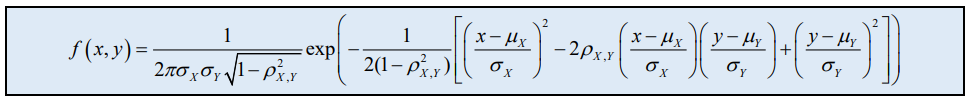
image-20240229222840222

概率密度函数 (Probability Density Function, PDF)

几何 (geometry)

微积分 (calculus)

线性代数 (linear algebra)

线性回归 (linear regression)

主成分分析 (principal component analysis)

相关性系数 (Pearson Correlation Coefficient, PCC)

条件概率分布 (conditional probability distribution)

马氏距离 (Mahalanobis distance) 考虑了数据的分布形状

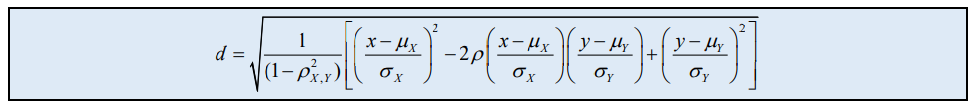
image-20240229223232410

欧氏距离 (Eucliean distance)

平移 (translation)

旋转 (rotation)

缩放 (scaling)

特征值分解 (Eigen Value Decomposition, EVD)

多元高斯分布 (multi-variate Gaussian distribution)

高斯判别分析 (Gaussian discriminant analysis)

高斯朴素贝叶斯 (Gaussian Naive Bayes)

高斯过程 (Gaussian process)

高斯混合模型 (Gaussian mixture model)

斜率 (slope)

截距 (intercept)

最小二乘法 (Ordinary Least Square, OLS) 最小化观测数据与模型预测值之间的残差平方和

范数、超定方程组、伪逆、QR 分解、SVD 分解

频率学派推断 (Frequentist inference)

贝叶斯学派推断 (Bayesian inference)

二元线性回归 (bivariate linear regression)

多元线性回归 (multi-variate linear regression)

过拟合 (overfitting)果一个模型在训练数据表现很好，但是在新数据上表现糟糕。不断引入变量会导致模型过于复杂，从而引发过拟合问题

正则化 (regularization)

多项式回归 (polynomial regression)

逻辑回 归 (logistic regression)

有监督学习 (supervised learning)回归是有监督学习任务的一种

无 监督学习 (unsupervised learning)。

分类 (classification)

—主成分 分析 (Principal Component Analysis, PCA)，解释正交回归的最好办法是机器学习中的一种常用降维算法

image-20240229224947673

image-20240229230200493

image-20240229230237212

image-20240229230354084

image-20240229230511243

image-20240229230525773

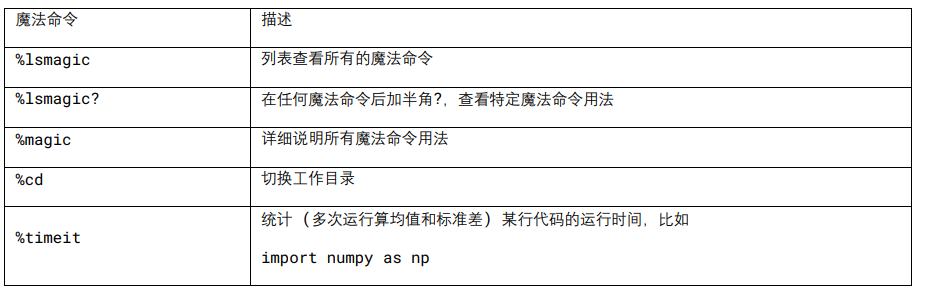
image-20240229230858432

image-20240229230942953

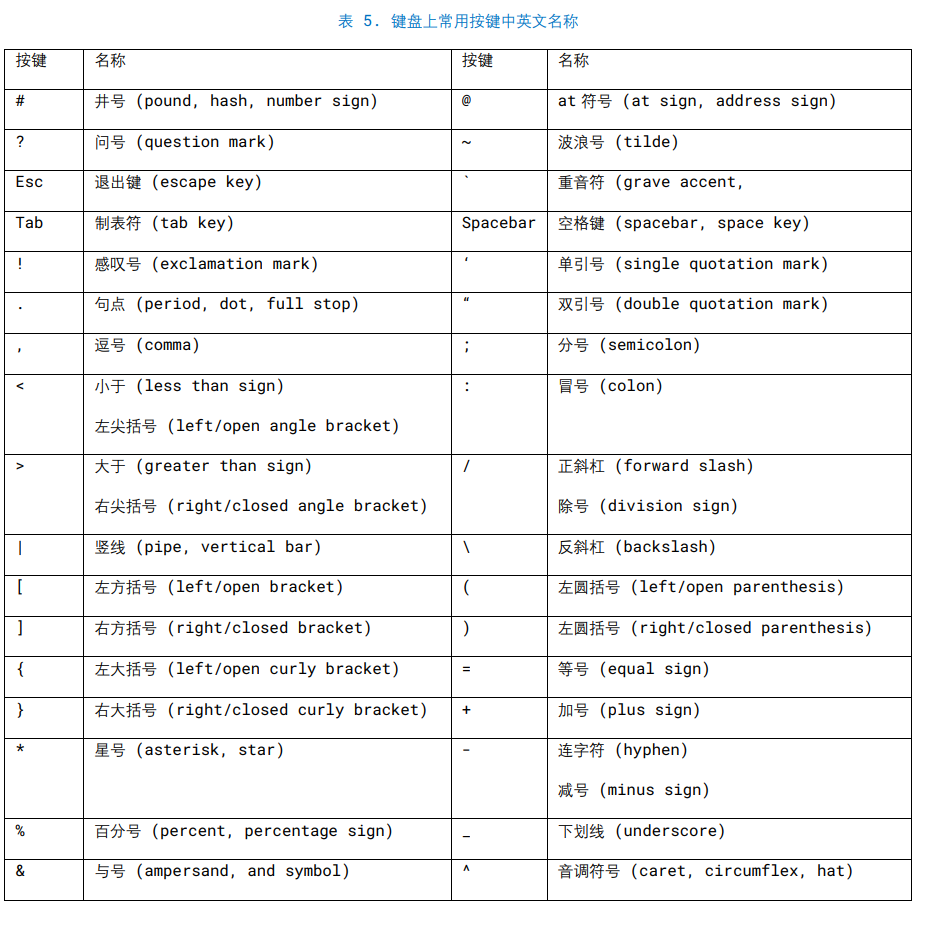
image-20240229231037097

LaTeX

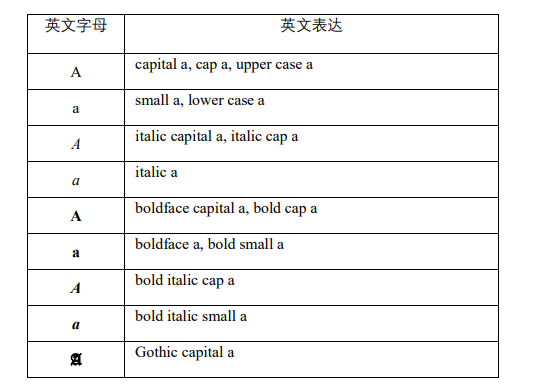
正体 aA (regular)

粗体 Aa (bold)

斜体 Aa (italic)

粗体斜体 Aa (bold italic)

无衬线体 (sans-serif)、衬线体 (serif)、花体 (calligraphy)、上标 Aa (superscript)、下标 Aa (subscript)。

无衬线体是指在字母末端没有装饰性衬线:设计更加简洁，直接， 没有额外的装饰.为在低分辨率的显示条 件下，无衬线体更容易阅读。常用的无衬线体字体有 Arial、Roboto 等Roboto 是 Google 开源字体.适合做注释

最常见的衬线字 体莫过于 Times New Roman。鸢尾花书中大量使用 Times New Roman，特别是在公式中

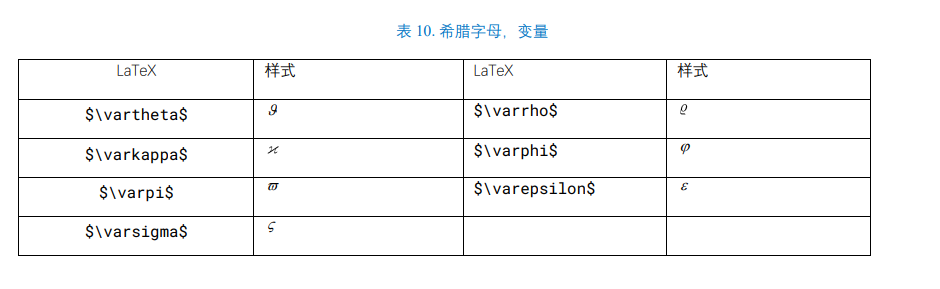
等宽字体 (monospaced font, Mono)

常见的 Mono 字体为 Courier New

image-20240229233032267

image-20240229233039956

image-20240229233056687

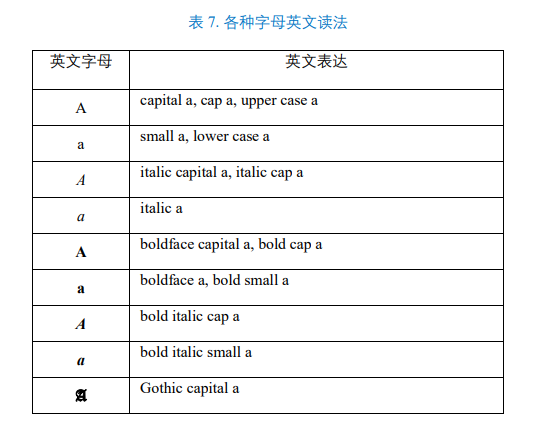
image-20240229233101873

image-20240229233525459

image-20240229233539530

image-20240229233547493

image-20240229233553160

image-20240229233558019

不间断连字符 (nonbreaking hyphen)、

− 减号 (minus sign)

、– 短破折号 (en dash)、

— 长破折号 (em dash)、

_ 下划线 (underscore)、

/ 前斜 线 (forward slash)、

\ 反斜线 (backward slash, backslash, reverse slash)、

| 竖 线 (vertical bar, pipe)

image-20240229233620229

image-20240229233630355

image-20240229233639435

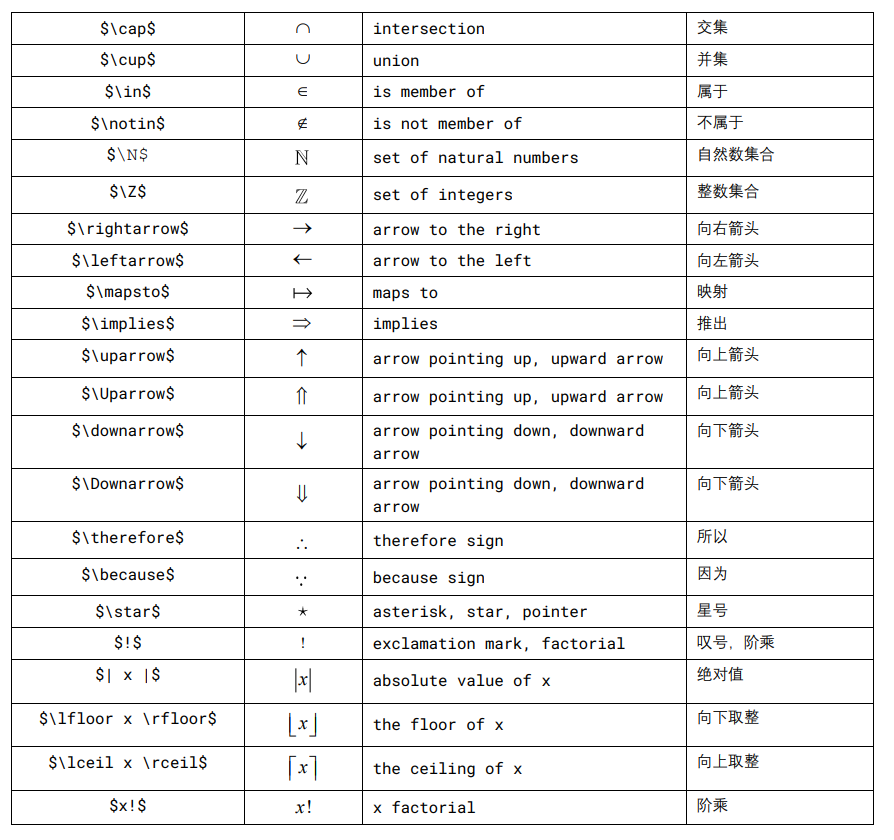
image-20240229233645440

$$A_{m\times n} =
\begin{bmatrix}
a_{1,1} & a_{1,2} & \cdots & a_{1,n} \
a_{2,1} & a_{2,2} & \cdots & a_{2,n} \
\vdots & \vdots & \vdots & \vdots\
a_{3,1} & a_{3,2} & \cdots & a_{3,n} \
\end{bmatrix}$$

$$f_X(x) = {\frac {1}{\sigma{\sqrt {2\pi}}}}
\exp \left({-{\frac {1}{2}}}
\left({\frac {x-\mu}{\sigma}}\right)^{2}\right)
$$

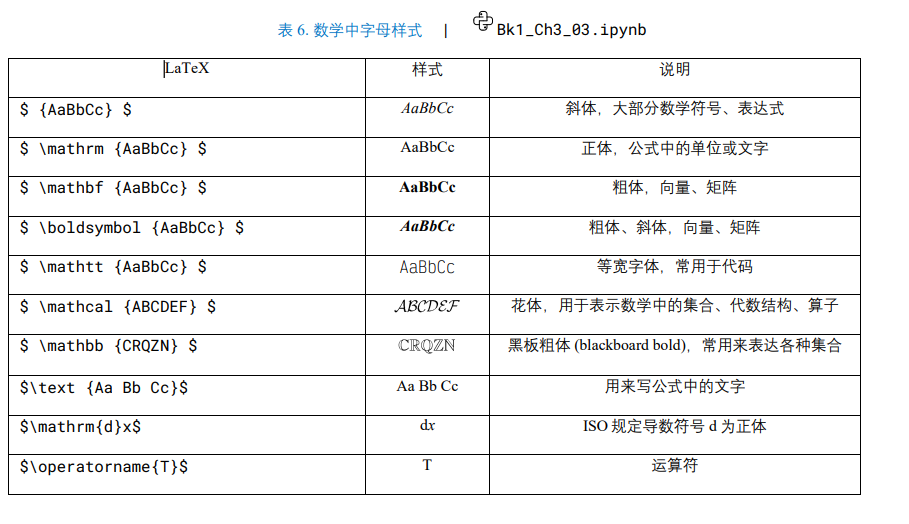
$${AaBbCc}$$
$$\mathrm{AaBbCc}$$
$$\mathbf{AaBbCc}$$
$$\boldsymbol{AaBbCc}$$
$$\mathtt{AaBbCc}$$
$$\mathcal{AaBbCc}$$
$$\mathbb{AaBbCc}$$
$$\text{AaBbCc}$$
$$\mathrm{d}x$$
$$\operatorname{T}$$

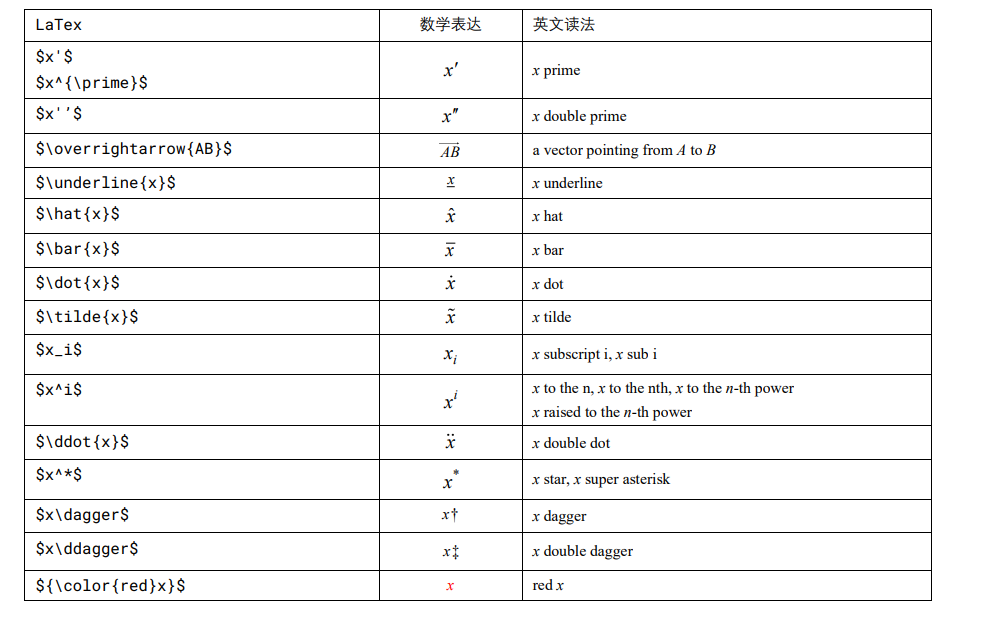
$$x’$$
$$x^\prime$$

$$x’’$$

$$\overrightarrow{AB}$$
$$\underline{AB}$$
$$\hat{AB}$$
$$\bar{AB}$$
$$\dot{AB}$$
$$\tilde{AB}$$
$$x_i$$
$$x^i$$
$$\ddot{x}$$
$$x^*$$
$$x\dagger$$
$$x\ddagger$$

$${\color{red}x}$$

$$)$$
$$]$$
$${$$
$$\pm$$
$$<$$
$$\geq$$
$$\gg$$
$$=$$
$$\equiv$$
$$\approx$$
$$\propto$$

$$\partial$$

$$\perp$$

$$\supseteq$$

$$x^{2}-y^{2} = \left(x+y\right)\left(x-y\right)$$$

$a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb+a_{2}x^{2}+a_{1}x+a_{0}$

$\sum_{k=0}^{n}a_{k}^{k}$

$ ax^{2}+bx+c=0\ (a\neq 0) $

${\sqrt[{n}]{a^{m}}}=(a^{m})^{1/n}=a^{m/n}=(a^{1/n})^{m} = ({\sqrt[{n}]{a}})^{m}$

${\sqrt[{n}]{a^{m}}}=(a^{m})^{1/n}=a^{m/n}=(a^{1/n})^{m}=({\sqrt[ {n}]{a}})^{m}$

$\left({\sqrt {1-x^{2}}}\right)^{2}$

$\frac {1}{x+1}+{\frac {1}{x-1}}={\frac {2x}{x^{2}- 1}}$

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

$f(x)=ax^{2}+bx+c{\text{ with }}a,b,c\in \mathbb {R} ,\ a\neq 0$

$f(x_1, x_2) = x_1^2 + x_2^2 + 2x_1x_2$

$\log_{b}(xy)=\log_{b}x+\log_{b}y$

$\ln(xy)=\ln x+\ln y{\text{ for }} x>0 {\text{ and }} y>0$

$f(x)=a\exp \left(-{\frac {(xb)^{2}}{2c^{2}}}\right)$

$\sin ^{2}\theta +\cos ^{2}\theta =1$

$\sin 2\theta =2\sin \theta \cos \theta$

$\sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$

$\tan(\alpha \pm \beta )=\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }$

$\exp(x)=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+\cdots $

$ \left(\sum {i=0}^{n}a{i}\right)\left(\sum {j=0}^{n}b{j}\right)=\sum {i=0}^{n}\sum {j=0}^{n}a{i}b{j}$

$\exp(x) =\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}$

$\frac {\mathrm{d}}{\mathrm{d}x} \exp(f(x)) =f’(x) \exp(f(x))$

$\int_{a}^{b}f(x) \mathrm {d} x$

$\int _{-\infty }^{\infty }\exp(- x^{2})\mathrm{d}x={\sqrt {\mathrm{\pi} }}$

$\int _{-\infty }^{\infty }\int _{- \infty }^{\infty } \exp \left({- \left(x^{2}+y^{2}\right)} \right) {\mathrm{d}x} {\mathrm{d}y} = \pi$

$\frac {\partial ^{2}f}{\partial x^{2}}=f’’_{xx}=\partial _{xx}f=\partial _{x}^{2}f$

${\frac {\partial ^{2}f}{\partial y \partial x}}={\frac {\partial }{\partial y}}\left({\frac {\partial f}{\partial x}}\right)=f’’_{xy}$

$\mathbf {a} = {\begin{bmatrix} a_{1} \ a_{2} \ a_{3} \end{bmatrix}} = [a_{1}\ a_{2}\ a_{3}]^{\operatorname {T} }$

$\left|\mathbf {a} \right|=\sqrt {a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$

$\mathbf {a} \cdot \mathbf {b} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$

$\mathbf {a} \cdot \mathbf {b} =\left|\mathbf {a} \right|\left|\mathbf {b} \right|\cos \theta $

$|\mathbf {x} |_{p}=\left(\sum {i=1}^{n}\left|x{i}\right|^{p}\right)^{1/p}$

$\mathbf {A} = {\begin{bmatrix} 1 & 2\ 3 & 4 \ 5 & 6 \end{bmatrix}}$

$\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\a_{21}&a_{22}&\cdots &a_{2n}\\vdots &\vdots &\ddots &\vdots \a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}$

$\left(\mathbf {A} +\mathbf {B} \right)^{\operatorname {T} }=\mathbf {A} ^{\operatorname {T} }+\mathbf {B} ^{\operatorname {T} }$

$\left(\mathbf {AB} \right)^{\operatorname {T} }=\mathbf {B} ^{\operatorname {T} }\mathbf {A} ^{\operatorname {T} }$

$ \left(\mathbf {A} ^{\operatorname {T} }\right)^{-1}=\left(\mathbf {A} ^{- 1}\right)^{\operatorname {T} }$

$\mathbf {u} \otimes \mathbf {v} = \mathbf {u} \mathbf {v} ^ {\operatorname {T}} = {\begin{bmatrix}u_{1} \ u_{2} \ u_{3} \ u_{4} \end{bmatrix}} {\begin{bmatrix} v_{1}&v_{2}&v_{3} \end{bmatrix}} = {\begin{bmatrix} u_{1}v_{1} & u_{1}v_{2} & u_{1}v_{3} \ u_{2}v_{1} & u_{2}v_{2} & u_{2}v_{3} \ u_{3}v_{1} & u_{3}v_{2} & u_{3}v_{3} \ u_{4}v_{1} & u_{4}v_{2} & u_{4}v_{3} \end{bmatrix}}$

$\det {\begin{bmatrix} a & b \ c & d \end{bmatrix}} = ad-bc$

$\Pr(A\vert B)={\frac {\Pr(B\vert A)\Pr(A)}{\Pr(B)}}$

$ f_{X\vert Y=y}(x)={\frac {f_{X,Y}(x,y)}{f_{Y}(y)}}$

$\operatorname {var} (X) = \operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}$

$\operatorname {var} (aX+bY)=a^{2}\operatorname {var} (X) + b^{2}\operatorname {var} (Y) + 2ab \operatorname {cov} (X,Y)$

$\operatorname {E} [X]=\int {- \infty }^{\infty }xf{X}(x) \operatorname {d}x$

$ X\sim N(\mu ,\sigma ^{2})$

$\frac {\exp \left(-{\frac {1}{2}}\left({\mathbf {x} }-{\boldsymbol {\mu }}\right)^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}\left({\mathbf {x} }- {\boldsymbol {\mu }}\right)\right)}{\sqrt {(2\pi )^{k}|{\boldsymbol {\Sigma }}|}}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83


-------------

$\left({\sqrt {1-x^{2}}}\right)^{2}$

$\frac {1}{x+1}+{\frac {1}{x-1}}={\frac {2x}{x^{2}- 1}}$

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

$f(x)=ax^{2}+bx+c~~{\text{ with }}~~a,b,c\in  \mathbb {R} ,\ a\neq 0$

$f(x_1, x_2) = x_1^2 + x_2^2 + 2x_1x_2$

$\log_{b}(xy)=\log_{b}x+\log_{b}y$

$\ln(xy)=\ln x+\ln y{\text{ for }} x>0  {\text{ and }} y>0$

$f(x)=a\exp \left(-{\frac {(xb)^{2}}{2c^{2}}}\right)$

$\sin ^{2}\theta +\cos ^{2}\theta =1$

$\sin 2\theta =2\sin \theta \cos \theta$

$\sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm  \cos \alpha \sin \beta$

$\tan(\alpha \pm \beta )=\frac {\tan \alpha \pm \tan  \beta }{1\mp \tan \alpha \tan \beta }$

$\exp(x)=\sum _{k=0}^{\infty }{\frac  {x^{k}}{k!}}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+\cdots $

$ \left(\sum _{i=0}^{n}a_{i}\right)\left(\sum  _{j=0}^{n}b_{j}\right)=\sum _{i=0}^{n}\sum  _{j=0}^{n}a_{i}b_{j}$

$\exp(x) =\lim _{n\to \infty }\left(1+{\frac  {x}{n}}\right)^{n}$

$\frac {\mathrm{d}}{\mathrm{d}x} \exp(f(x)) =f'(x)  \exp(f(x))$

$\int_{a}^{b}f(x) \mathrm {d} x$

$\int _{-\infty }^{\infty }\exp(- x^{2})\mathrm{d}x={\sqrt {\mathrm{\pi} }}$

$\int _{-\infty }^{\infty }\int _{- \infty }^{\infty } \exp \left({- \left(x^{2}+y^{2}\right)} \right) {\mathrm{d}x}  {\mathrm{d}y} = \pi$

$\frac {\partial ^{2}f}{\partial  x^{2}}=f''_{xx}=\partial _{xx}f=\partial _{x}^{2}f$

${\frac {\partial ^{2}f}{\partial y \partial  x}}={\frac {\partial }{\partial y}}\left({\frac  {\partial f}{\partial x}}\right)=f''_{xy}$

$\mathbf {a} = {\begin{bmatrix} a_{1} \\ a_{2} \\ a_{3} \end{bmatrix}} = [a_{1}\ a_{2}\ a_{3}]^{\operatorname {T} }$

$\left\|\mathbf {a} \right\|=\sqrt  {a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$

$\mathbf {a} \cdot \mathbf {b} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$

$\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a}  \right\|\left\|\mathbf {b} \right\|\cos \theta $

$\|\mathbf {x} \|_{p}=\left(\sum  _{i=1}^{n}\left|x_{i}\right|^{p}\right)^{1/p}$

$\mathbf {A} = {\begin{bmatrix} 1 & 2\\ 3  & 4 \\ 5 & 6 \end{bmatrix}}$

$\mathbf {A}  ={\begin{bmatrix}a_{11}&a_{12}&\cdots  &a_{1n}\\a_{21}&a_{22}&\cdots  &a_{2n}\\\vdots &\vdots &\ddots &\vdots  \\a_{m1}&a_{m2}&\cdots  &a_{mn}\end{bmatrix}}$

$\left(\mathbf {A} +\mathbf {B}  \right)^{\operatorname {T} }=\mathbf {A}  ^{\operatorname {T} }+\mathbf {B}  ^{\operatorname {T} }$

$\left(\mathbf {AB}  \right)^{\operatorname {T} }=\mathbf {B}  ^{\operatorname {T} }\mathbf {A}  ^{\operatorname {T} }$

$ \left(\mathbf {A} ^{\operatorname  {T} }\right)^{-1}=\left(\mathbf {A} ^{- 1}\right)^{\operatorname {T} }$

$\mathbf {u} \otimes \mathbf {v} = \mathbf {u} \mathbf {v} ^ {\operatorname  {T}} = {\begin{bmatrix}u_{1} \\ u_{2} \\ u_{3} \\ u_{4} \end{bmatrix}} {\begin{bmatrix} v_{1}&v_{2}&v_{3} \end{bmatrix}} = {\begin{bmatrix} u_{1}v_{1} & u_{1}v_{2} & u_{1}v_{3} \\ u_{2}v_{1} & u_{2}v_{2} & u_{2}v_{3} \\ u_{3}v_{1} & u_{3}v_{2} & u_{3}v_{3} \\ u_{4}v_{1} & u_{4}v_{2} & u_{4}v_{3} \end{bmatrix}}$

$\det {\begin{bmatrix} a & b \\ c & d  \end{bmatrix}} = ad-bc$

$\Pr(A\vert B)={\frac {\Pr(B\vert  A)\Pr(A)}{\Pr(B)}}$

$ f_{X\vert Y=y}(x)={\frac  {f_{X,Y}(x,y)}{f_{Y}(y)}}$

$\operatorname {var} (X) = \operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}$

$\operatorname {var} (aX+bY)=a^{2}\operatorname  {var} (X) + b^{2}\operatorname {var} (Y) + 2ab  \operatorname {cov} (X,Y)$

$\operatorname {E} [X]=\int _{- \infty }^{\infty }xf_{X}(x) \operatorname {d}x$

$ X\sim N(\mu ,\sigma ^{2})$

$\frac {\exp \left(-{\frac  {1}{2}}\left({\mathbf {x} }-{\boldsymbol  {\mu }}\right)^{\mathrm {T} }{\boldsymbol  {\Sigma }}^{-1}\left({\mathbf {x} }- {\boldsymbol {\mu }}\right)\right)}{\sqrt  {(2\pi )^{k}|{\boldsymbol {\Sigma }}|}}$

numpy科学计算。它提供了一个高性能的多维数组对象，以及用于操作这些数组的各种工具。NumPy 是许多高级数据分析和科学计算库的基础，包括 Pandas、SciPy、Matplotlib、scikit-learn、scikit-image 等，因为它提供了快速且高效的数组操作能力

plotly.express是 Plotly 库的一个高级接口，快速且简单的方式来创建各种交互式图表和数据可视化。它支持一系列图表类型，如线图、散点图、柱状图、箱型图、热力图、3D 图等。Plotly 生成的图表是交互式的，支持缩放、平移、悬浮提示等。简洁的 API，仍可以通过访问底层的 Plotly 图表对象来进行高度的自定义。

Matplotlib.pyplot

  • 目的：matplotlib.pyplot是一个绘图库，可在多种硬拷贝格式和交互环境中生成出版质量的图形。它可以在Python脚本、Python和IPython shell、Jupyter笔记本、Web应用服务器以及四种图形用户界面工具包中使用。

  • 主要特点

    ：

    • 仅需几行代码即可生成图表、直方图、功率谱、条形图、误差图、散点图等。
    • 对于简单的绘图，pyplot模块提供了类似MATLAB的界面。
    • 高度可定制和扩展。

numpy.arange([start, ]stop, [step, ]dtype=None)

  • start：区间的起始值，默认为 0。
  • stop：区间的终止值（不包括）。
  • step：两个值之间的间隔，默认为 1。
  • dtype：数组的数据类型，如果不指定，则由输入数据的类型决定。

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)

  • start：序列的起始值。
  • stop：序列的结束值。
  • num：要生成的等间隔样本数量，默认是50。
  • endpoint：布尔值，如果为True，则序列包含stop值；如果为False，则不包含结束值，默认是True。
  • retstep：布尔值，如果为True，则返回样本和步长；如果为False，则只返回样本，默认是False。
  • dtype：数组的类型。如果未指定，则推断出输出数组的数据类型。
  • axis：在多维数组的哪个轴上创建值的间隔，0 表示第一个轴。
  • 结束点：np.arange 不包含结束值，而 np.linspace 默认包含结束值。
  • 间隔：np.arange 通过步长来控制间隔，np.linspace 通过指定数量来控制间隔。
  • 用途：当你关心数组的“步长”时，np.arange 更加有用；当你关心数组中要包含的元素数量时，np.linspace 更合适。
1
2
3
4
5
np.arange(0, 10, 2)
> [0, 2, 4, 6, 8]

np.linspace(0, 10, 5)
> [0.0, 2.5, 5.0, 7.5, 10.0]

np.meshgrid用于生成两个（或更多）数组，其中一个数组是所有的 x 坐标，另一个数组是所有的 y 坐标。这些数组可以用来作为网格的基础，进而可以在整个网格上计算某个函数的值。绘制二维、三维图形和进行矩阵运算

plt.figure()创建一个新的图形或激活一个现有图形。这个函数是绘图过程的开始，提供了一个画布，之后可以在上面绘制各种图形（如线图、散点图、条形图等）和添加图形元素（如标题、标签和图例）。

  • figsize：一个元组，指定图形的宽度和高度，单位为英寸。
  • dpi：图形的分辨率，以每英寸点数表示。
  • facecolor：图形的背景颜色。
  • edgecolor：图形边缘的颜色。

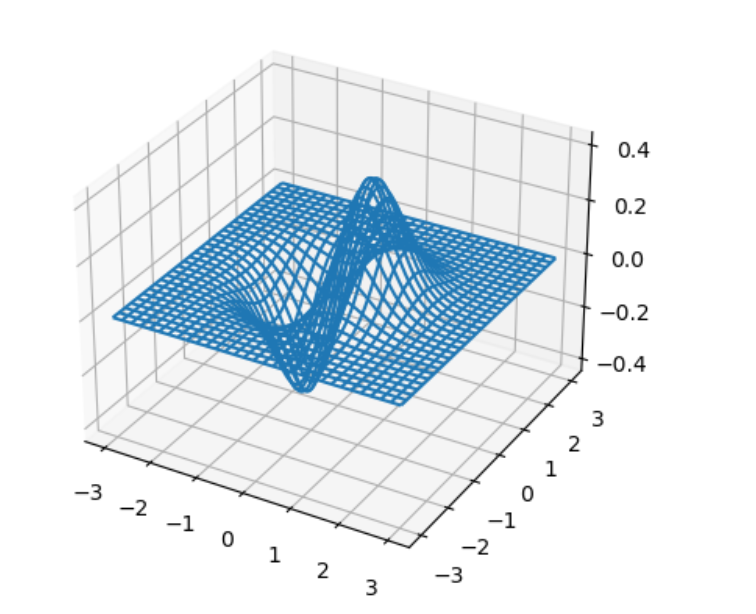
ax = fig.add_subplot(projection='3d') 这行代码的作用是在图形窗口中添加一个三维子图。这里，fig 是通过 plt.figure() 创建的图形对象，而 ax 是添加到图形中的子图（或称为轴域），它具有三维绘图的能力。让我们通过一个简单的例子来解释这个过程：

ax.plot_wireframe(xx1, xx2, ff, rstride=10, cstride=10)用于绘制三维线框图的方法。这个方法特别适用于展示三维曲面的结构，比如数学函数的图形或者三维数据的可视化。在这个上下文中，xx1、xx2 和 ff 分别代表了网格上的 X、Y 坐标和对应的 Z 值（或者说高度）。rstride 和 cstride 参数用来控制行和列的步进，决定了绘制线框时的密集程度。

fig = plt.figure()
ax = fig.add_subplot(projection=’3d’)

绘制二元函数网格曲面

ax.plot_wireframe(xx1, xx2, ff, rstride=10, cstride=10)

plt.show()

image-20240301181500580

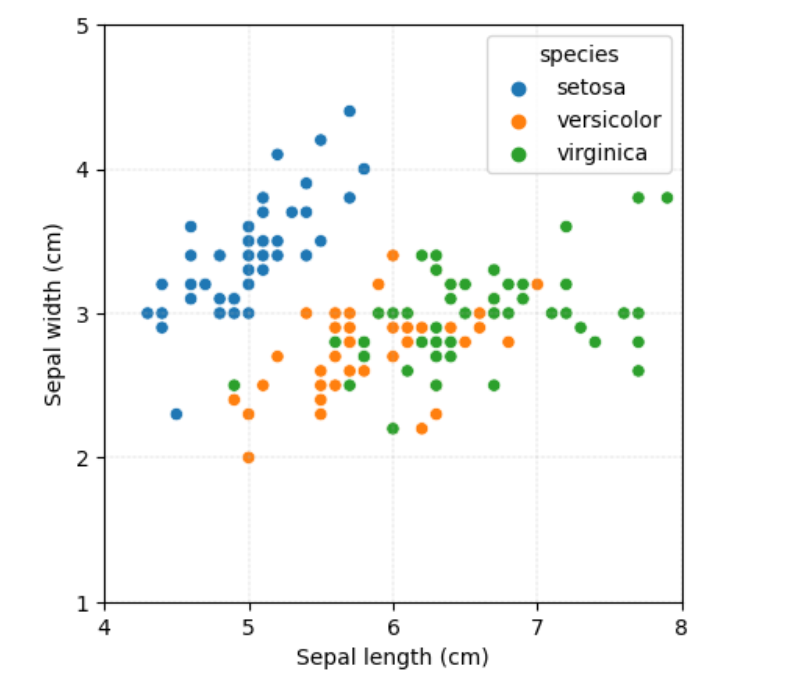
fig, ax = plt.subplots()

ax = sns.scatterplot(data=iris_df, x=”sepal_length”,
y=”sepal_width”, hue = “species”)

hue 用不同色调表达鸢尾花的类别

ax.set_xlabel(‘Sepal length (cm)’)
ax.set_ylabel(‘Sepal width (cm)’)
ax.set_xticks(np.arange(4, 8 + 1, step=1))
ax.set_yticks(np.arange(1, 5 + 1, step=1))
ax.axis(‘scaled’)
ax.grid(linestyle=’-.’, linewidth=0.25, color=[0.7,0.7,0.7])
ax.set_xbound(lower = 4, upper = 8)
ax.set_ybound(lower = 1, upper = 5)

image-20240301181531625

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import ploty.graph_objects as go
fig = go.Figure(data = [go.Surface(z=ff,x=x1_array,y = x2_array,colorscale='RdYlBu_r')])
fig.update_layout(autosize=False,
                  width=800, height=800,
                  margin=dict(l=65, r=50, b=65, t=90))
fig.show()

# 以下是ChatGPT对代码的解释：
# 这几句代码是在使用 Python 编程语言中的 Plotly 库来创建并展示一个三维表面图。
# 具体来说，代码的意思如下：
# 第一行代码中，我们导入了 Plotly 库中的图形对象模块，并将其重命名为“go”，以方便在代码中引用。
# 第二行代码中，我们创建了一个 Figure 对象，它将包含我们要绘制的三维表面图。
# 在这个 Figure 对象中，我们传递了一个 data 参数，其中包含我们要绘制的表面图数据。
# 具体来说，我们使用了 Surface 对象来表示这个表面图，传递了三个参数：
# z 代表 z 轴的数值数据，x 代表 x 轴的数值数据，y 代表 y 轴的数值数据，colorscale 代表颜色映射的方案。
# 第三行代码中，我们使用 update_layout() 方法来设置图形的布局。
# 具体来说，我们设置了图形的尺寸为 800*800，同时指定了图形的边距和位置等信息。
# 第四行代码中，我们使用 show() 方法来显示绘制好的图形。
# 需要注意的是，代码中的变量 ff、x1_array、x2_array 都是在代码之前定义好的，并包含了我们要绘制的表面图的数据信息。

image-20240301182531617

assert断言

boolean布尔值

lambda匿名

raise引发异常

tuple元组

yield产生

注释 (comment)

解释器 (interpreter)

# (hash, hashtag, hashmark)

‘’’或”””注释：多行

冒号 (colon)

分号 (semi-colon)

缩进 (indentation)

索引和切片：

1
2
3
4
string_obj[start:end:step_size] # 字符串
list_obj[start:end:step_size] # 列表
tuple_obj[start:end:step_size] # 元组
numpy_array[start:end:step_size] # NumPy array

字典键值对:

1
dict_obj{key:value} # 字典

lambda 函数 :

1
lambda variables: expression

定义类:

1
2
class ClassName:
 # 代码块，注意缩进

异常处理：

1
2
3
4
5
6
try:
 # 代码块，注意缩进
except SomeException:
 # 代码块，注意缩进
finally:
 # 代码块，注意缩进

上下文管理:

1
2
with context_manager:
 # 代码块，注意缩进；第 35 和 36 章中使用 streamlit 库时会用到

缩进 (indentation)

流程图 (flowchart)

实数轴 (number line)

箭头 (flowline, arrowhead)

科学 计数法 (scientific notation)

于遍历 (iterate)

可迭代对象 (iterator)

驼峰命名法 (camelCase)

下划线分隔法 (snake_case)

Pythonic

image-20240301190658407

索引 (indexing)

切片 (slicing)

image-20240301191019685

图例 (legend)

占位符 (placeholder)

是二进制 (binary numerical system

八进制 (octal numeral system) 和十六进制 (hexadecimal numeral system 或 hexadecimal 或 hex)

image-20240301192116971

圆括号 (parentheses)

视图 (view)

位运算符 (bitwise operator)

math 库

等差数列 (arithmetic progression)

注释 (annotation)

示原始字符串 (raw string)

exp：画正弦曲线

  • 上下限

    x_start = 0 # 弧度值

    x_end = 2*math.pi # 弧度值

    步数/分辨率

    step = (x_end - x_start) / (num - 1)

    X轴坐标点

    x_array = [x_start + i * step for i in range(num)]

    等长全0列表，用于测试X

    zero_array = [0 for i in range(num)]

    可视化等差数列

    plt.plot(x_array, zero_array, marker = ‘.’,
    markersize = 8,
    markerfacecolor=”w”,
    markeredgecolor=’k’)
    plt.text(x_start, 0, ‘0’)
    plt.text(x_end, 0, r’$2\pi$’)
    plt.axis(‘off’)
    plt.show()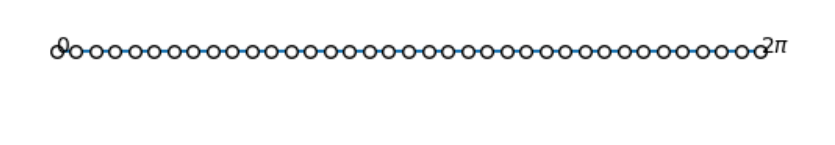

    image-20240301194527111

    Y轴坐标点

    y_array = [math.sin(x_idx) for x_idx in x_array]

    可视化正弦函数

    plt.plot(x_array, y_array, marker = ‘.’,
    markersize = 8,
    markerfacecolor=”w”,
    markeredgecolor=’k’)
    plt.text(x_start, -0.1, ‘0’)
    plt.text(x_end, 0.1, r’$2\pi$’)
    plt.axhline(y=0, color=’k’, linestyle=’–’, linewidth=0.25)
    plt.axis(‘off’)
    plt.show()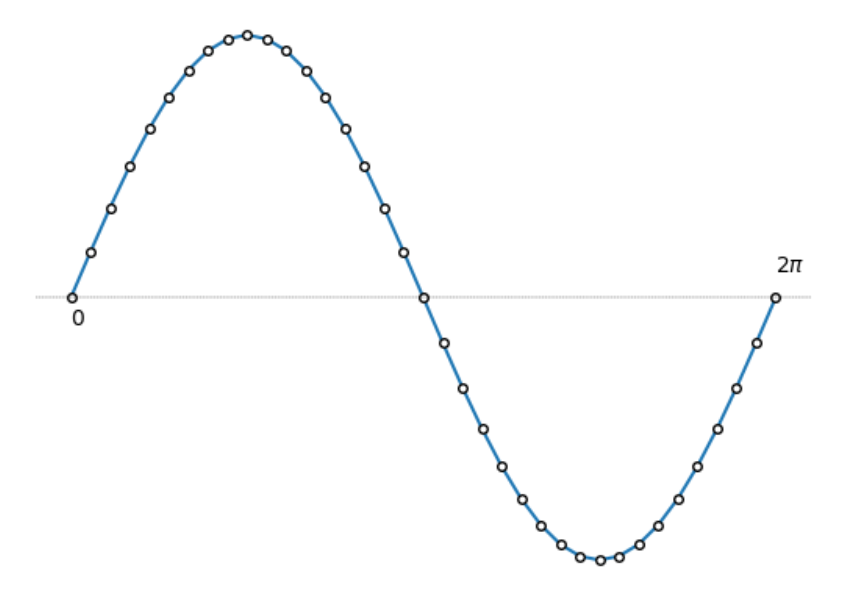

    image-20240301194616425

random 库和 statistics 库

提供了伪随机数生成器，通常用于模拟随机事件、生成 随机数据、进行随机采样等任务。

image-20240301194914283

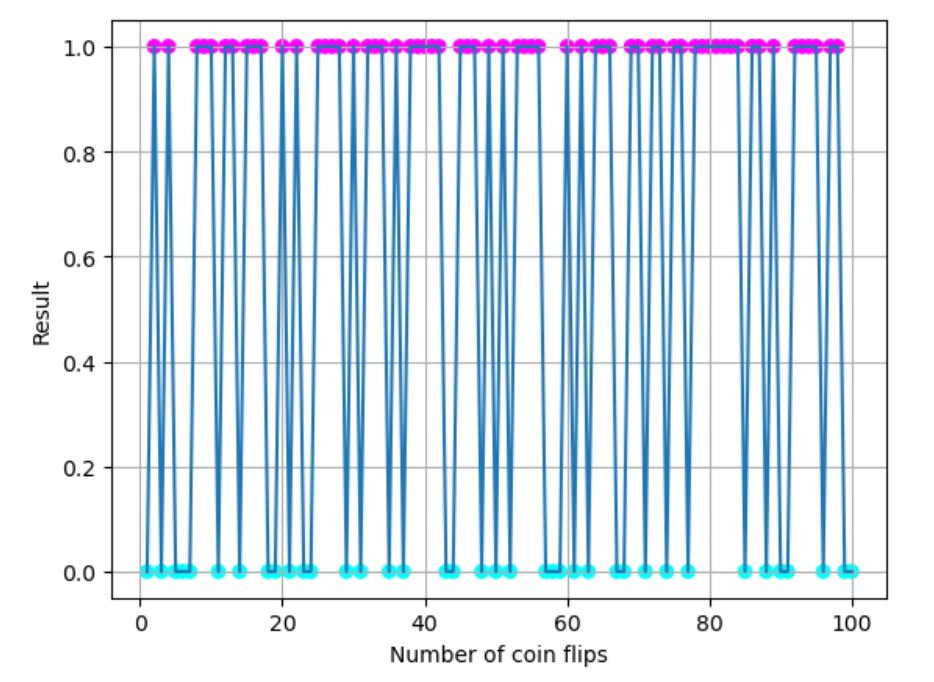
模拟了抛硬币的实验，并记录每次抛硬币后的结果，然后计算当前所有结果均值

反映了均值随时间的演化过程。随着抛硬币次数的增加，均值逐渐趋于 0.5，这是因为 硬币正反面出现的概率是相等的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 抛硬币实验的次数
num_flips = 1000

# 用于存储每次抛硬币的结果
results = []  
# 用于存储每次抛硬币后的均值
running_means = []  

for _ in range(num_flips):
    # 随机抛硬币，1代表正面 (H)，0代表反面 (T)
    result_idx = random.randint(0, 1)
    results.append(result_idx)

    # 计算当前所有结果的均值
    mean_idx = statistics.mean(results)
    running_means.append(mean_idx)
   
 # 可视化前100次结果均值随次数变化
visual_num = 100
plt.scatter(range(1, visual_num + 1), results[0:visual_num],
           c=results[0:visual_num],marker="o", cmap = 'cool')
plt.plot(range(1, visual_num + 1), results[0:visual_num])
plt.xlabel("Number of coin flips")
plt.ylabel("Result")
plt.grid(True)
plt.show()

# 可视化均值随次数变化
plt.plot(range(1, num_flips + 1), running_means)
plt.axhline(0.5, color = 'r')
plt.xlabel("Number of coin flips")
plt.ylabel("Running Mean")
plt.grid(True)
plt.ylim(0,1)
plt.show()

假设硬币不均匀，抛掷结果为 1 的概率为 0.6，为 0 的概率为 0.4

1
2
3
4
5
6
7
# 模拟抛硬币实验，硬币头重脚轻
# 用于存储每次抛硬币的结果
results = [random.choices([0, 1], [0.4, 0.6])[0] 
           for _ in range(num_flips)]
# 用于存储每次抛硬币后的均值
running_means = [statistics.mean(results[0:idx+1]) 
                 for idx in range(num_flips)]

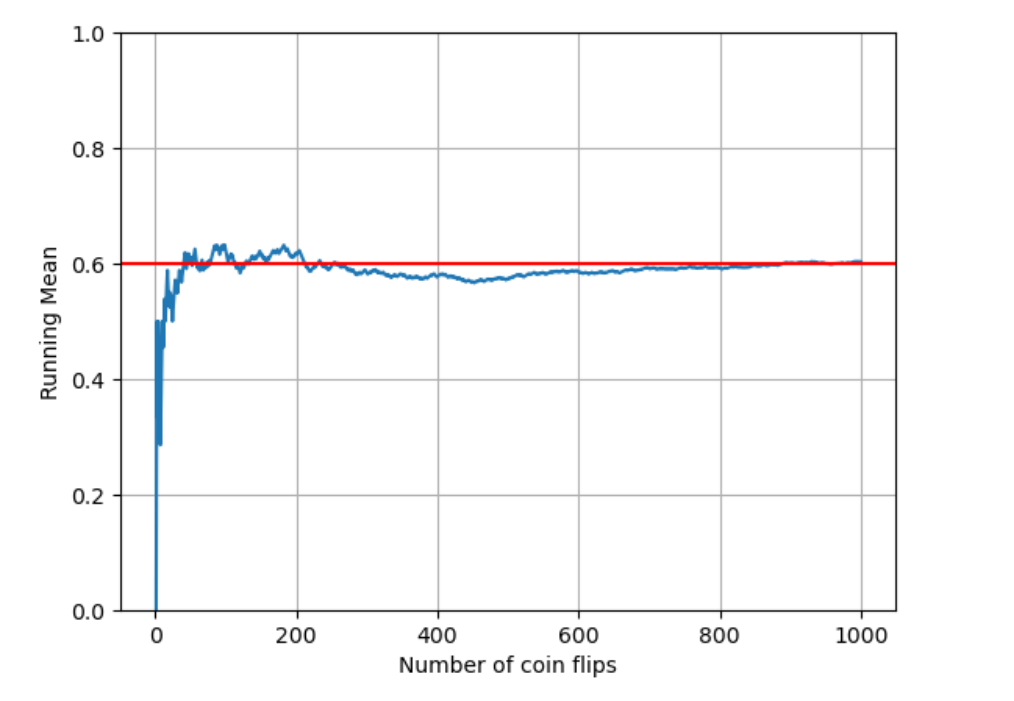
image-20240301200805420

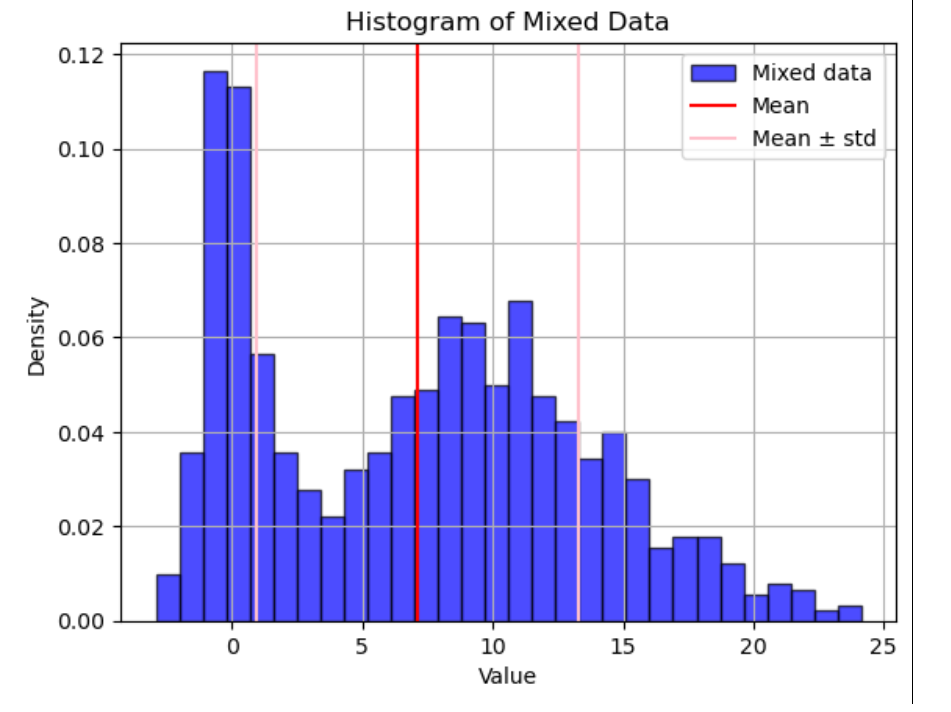
直方图 (histogram)。

概率 (probability)

概率密度 (probability density 或 density)

混合两个一元高斯分布随机数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
random.seed(0) # 方便复刻结果
# 生成300个服从N(0, 1**2)的随机数
mean1, std1, size1 = 0, 1, 300
data1 = [random.gauss(mean1, std1) for _ in range(size1)]
data1 = np.random.normal(mean1, std1, size1)
# data1 = [random.gauss(mean1, std1) for _ in range(size1)]

# 将两组随机数混合
mixed_data = data1 + data2
mean_loc = statistics.mean(mixed_data)
std_loc  = statistics.stdev(mixed_data)

# 绘制混合数据的直方图
plt.hist(mixed_data, bins=30, density=True, edgecolor='black', 
         alpha=0.7, color='blue', label='Mixed data')
plt.axvline(mean_loc, color = 'red', label='Mean')
plt.axvline(mean_loc + std_loc, 
            color = 'pink', label='Mean ± std')
plt.axvline(mean_loc - std_loc, color = 'pink')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.title('Histogram of Mixed Data')
plt.grid(True)
plt.show()

image-20240301201058141

线性回归：

1
2
3
4
5
6
7
8
9
10
11
12
13
# 这是确定散点

num = 50
np.random.seed(0)
# X上散点
x_data = [random.uniform(0, 10) for _ in range(num)]
#高斯分布的散点噪音
noise =  [random.gauss(0,1) for _ in range(num)]
y_data = [0.5 * x_data[idx] + 1 + noise[idx]
          for idx in range(num)]



1
2
3
4
5
6
7
fig, ax = plt.subplots()
ax.scatter(x_data, y_data)
ax.set_xlabel('x'); ax.set_ylabel('y')
ax.set_aspect('equal', adjustable='box')
ax.set_xlim(0,10); ax.set_ylim(-2,8)
ax.grid()

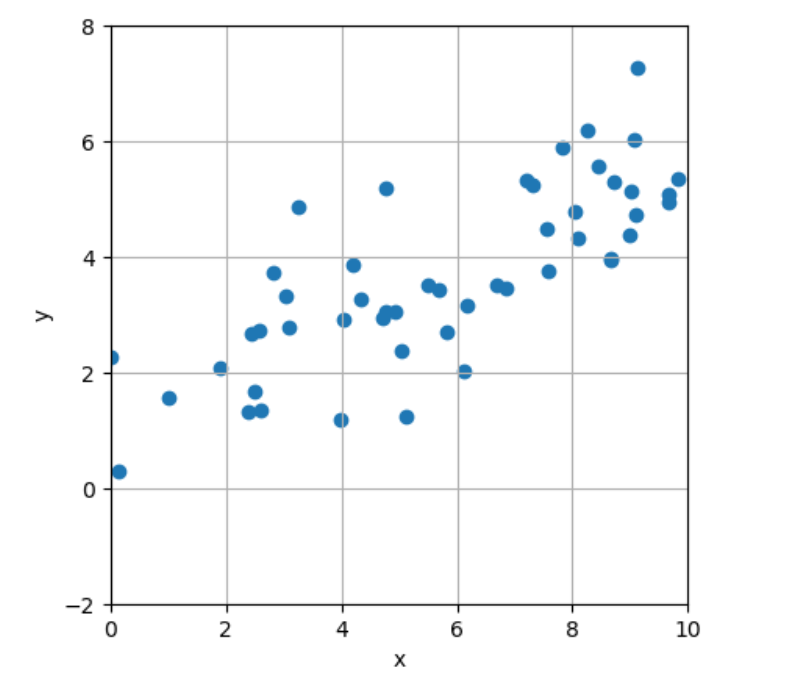
image-20240301201605871

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
slope, intercept = statistics.linear_regression(x_data, y_data)	#最核心的公式	


# 生成一个等差数列
start, end, step = 0, 10, 0.5
x_array = []
x_i = start

while x_i <= end:
    x_array.append(x_i)
    x_i += step
    
    # 计算x_array预测值
y_array_predicted = [slope * x_i + intercept for x_i in x_array]
    
    
# 可视化一元线性回归直线
fig, ax = plt.subplots()
ax.scatter(x_data, y_data)
ax.plot(x_array, y_array_predicted, color = 'r')
ax.set_xlabel('x'); ax.set_ylabel('y')
ax.set_aspect('equal', adjustable='box')
ax.set_xlim(0,10); ax.set_ylim(-2,8)
ax.grid()

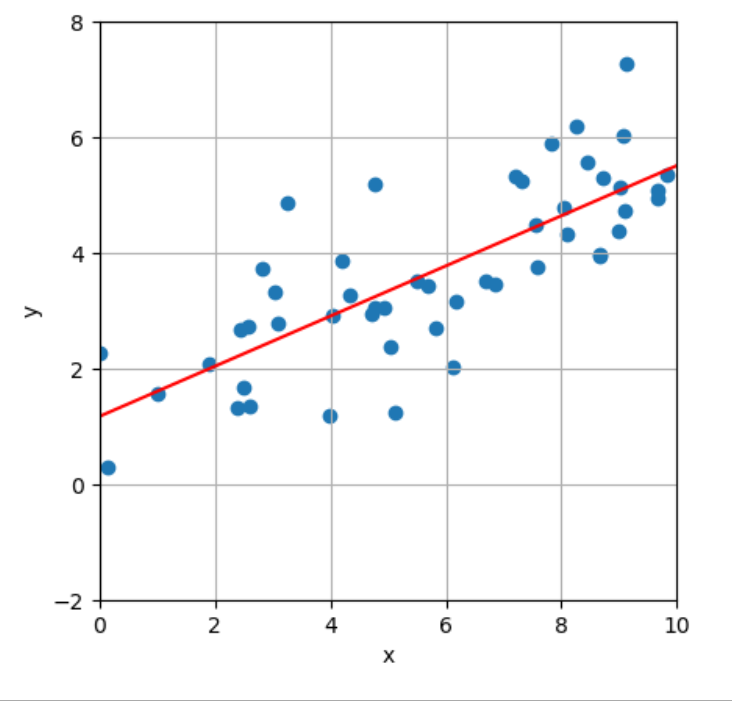
image-20240301201825520

捕捉异常

1
2
3
4
5
try:
    x = 1 / 0

except ZeroDivisionError:
    print("除数不能为零")

使用enumerate()

1
2
3
# 从1开始编号
for index, fruit in enumerate(fruits,1):
    print(index, fruit)

使用zip() 同步遍历多个对象

1
2
3
4
5
names = ['Alice', 'Bob', 'Charlie']
scores = [80, 90, 75]

for name, score in zip(names, scores):
    print(name, score)

image-20240301202919563

映射 (mapping)

定义域 (domain)

单射 (injective)

非单射 (non-injective)

满射 (surjective)

非满射 (non-surjective)

双射 (bijective)

一元函数 (unary function)

二元函数 (binary function)

三元函数 (ternary function)

多元函数 (n-ary function)

使用 assert 语句：插入断言，检查条件

1
2
3
4
5
6
7
8
9
10
assertion
# 定义除法函数
def divide(a, b):
 assert b != 0, "除数不能为零"
 return a / b
# 调用自定义函数
result = divide(10, 0) 
# 除以零，会引发 AssertionError 异常
print(result) 
# 上行不会被执行，因为异常已经引发

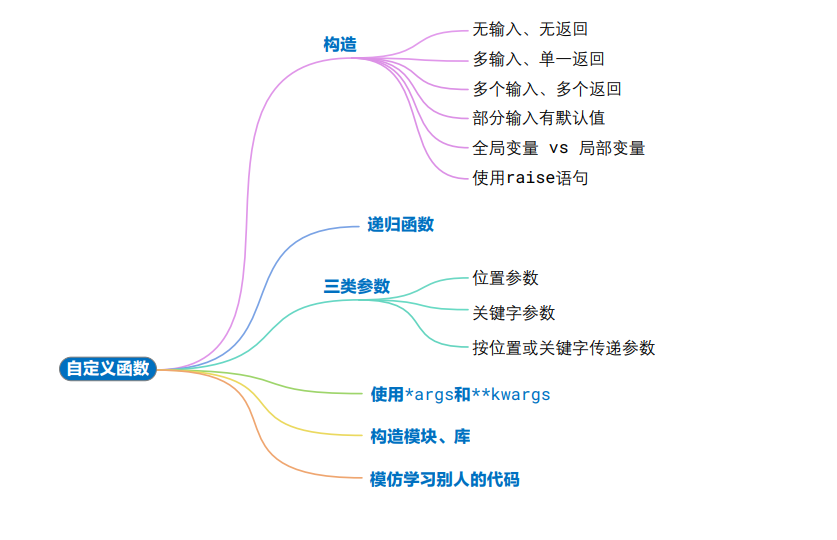
成阶乘 (factorial)

位置参数 (positional arguments)

关键字参数 (keyword arguments)

按位置或关键字传递参数 (positional or keyword arguments)

一个星号 * 常用来拆包 (unpacking)。它的作用是将一个可迭代对象，比如列 表、元组等，中的元素分别传递给函数的位置参数。

Statsmodels:

最小二乘线性回归 (Ordinary Least Square Regression)

方差分析 (Analysis of Variance, ANOVA)

主成分分析 (Principal Component Analysis, PCA)。

时间序列分析 (Timeseries Analysis)，如 ARIMA 模型。

非参数方法 (Nonparametric Methods)，比如核密度估计 (Kernel Density Estimation, KDE)。

统计假设检验 (statistical hypothesis testing)。

分位图，又称 QQ 图 (Quantile-Quantile plot)

image-20240301203856367

置信区间 (confidence interval)

置信水平 (confidence level)。

置信区间是一个范围，用于表示对一个未知参数的估计。一个 95% 的置信区间意味着我们有 95% 的置信度认为真实的参数值位于该区间内。

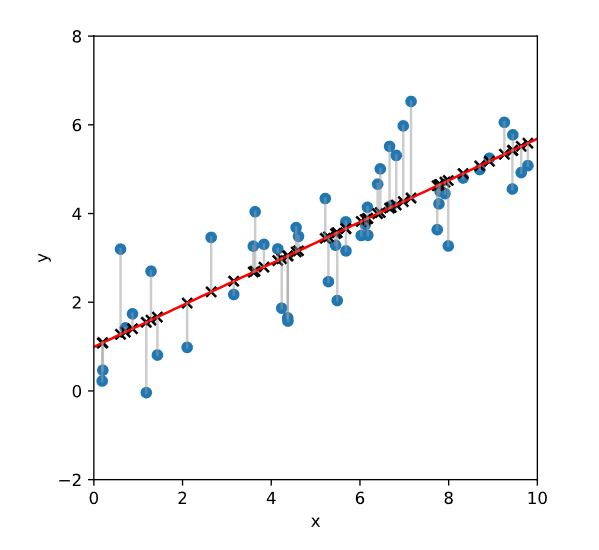
最小二乘线性回归:Ordinary Least Square, OLS linear regression

在最小二乘线性回归中，我们尝试找到一条直线，使得所有数据点到这条线的 距离之和最小。

这里的“距离”通常是指因变量与回归线预测值之间的差异，称为残差。

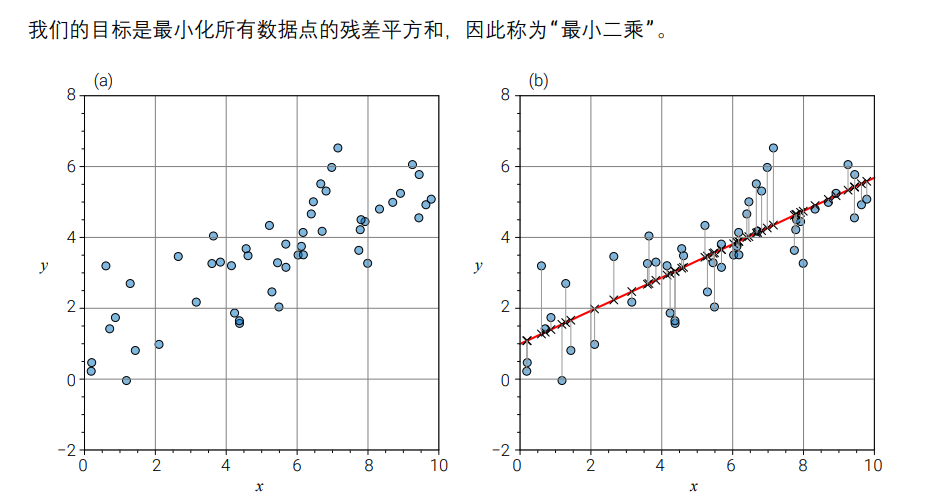
image-20240301204836505

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

# 生成随机数据
num = 50
np.random.seed(0)
x_data = np.random.uniform(0,10,num)
y_data = 0.5 * x_data + 1 + np.random.normal(0, 1, num)
data = np.column_stack([x_data,y_data])
# 添加常数列
X = sm.add_constant(x_data)
# 创建一元OLS线性回归模型
model = sm.OLS(y_data, X)
# 拟合模型
results = model.fit()
# 打印回归结果
print(results.summary())


# 预测
x_array = np.linspace(0,10,101)
predicted = results.params[1] * x_array + results.params[0]

fig, ax = plt.subplots()
ax.scatter(x_data, y_data)
ax.scatter(x_data, results.fittedvalues, 
           color = 'k', marker = 'x')
ax.plot(x_array, predicted, 
        color = 'r')

data_ = np.column_stack([x_data,results.fittedvalues])

ax.plot(([i for (i,j) in data_], [i for (i,j) in data]),
        ([j for (i,j) in data_], [j for (i,j) in data]),
        c=[0.6,0.6,0.6], alpha = 0.5)

ax.set_xlabel('x'); ax.set_ylabel('y')
ax.set_aspect('equal', adjustable='box')
ax.set_xlim(0,10); ax.set_ylim(-2,8)
# fig.savefig('一元线性回归.svg', format='svg')

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:决定系数                 0.656
Model:                            OLS   Adj. R-squared:调整后的决定系数     0.649
Method:                 Least Squares   F-statistic:     F 统计量         91.59
Date:                Fri, 01 Mar 2024   Prob(F-statistic):F统计量的概率值1.05e-12
Time:                        20:46:51   Log-Likelihood: 对数似然比      -67.046
No. Observations:                  50   AIC:    赤池信息准则              138.1
Df Residuals:  残差自由度            48   BIC:    贝叶斯信息准则            141.9
Df Model:       模型自由度            1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.9928      0.296      3.358      0.002       0.398       1.587
x1             0.4693      0.049      9.570      0.000       0.371       0.568
==============================================================================
Omnibus:                        1.199   Durbin-Watson:                   2.274
Prob(Omnibus):                  0.549   Jarque-Bera (JB):                1.213
Skew:                           0.283   Prob(JB):                        0.545
Kurtosis:                       2.487   Cond. No.                         13.6
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

OLS回归结果解释

  • Dep. Variable (因变量): y 表明模型预测的因变量是 y。
  • R-squared (决定系数): 0.656 指模型解释了因变量变异的 65.6%。这是衡量模型拟合优度的一个关键指标。
  • Adj. R-squared (调整后的决定系数): 0.649 考虑了模型中变量的数量，提供了另一个衡量拟合优度的指标。
  • F-statistic (F 统计量): 91.59 表示模型整体的统计显著性。
  • Prob (F-statistic) (F 统计量的概率值): 1.05e-12 显著小于0.05，意味着模型至少有一个预测变量对因变量有显著影响。
  • Log-Likelihood (对数似然比): -67.046 表示模型拟合的好坏，通常用于比较不同模型。
  • AIC (赤池信息准则) 和 BIC (贝叶斯信息准则): 分别是 138.1 和 141.9，用于模型选择，数值越小表示模型越优。
  • Df Residuals (残差自由度): 48 表示模型中残差的自由度。
  • Df Model (模型自由度): 1 表示模型中变量的数量。

系数部分

  • const: 0.9928 是截距项的估计值，标准误为 0.296，显著性水平 P>|t| 为 0.002，表示截距显著不为0。
  • x1: 0.4693 是自变量 x1 的系数估计，标准误为 0.049，显著性水平 P>|t| 为 0.000，表示 x1 对 y 有显著的正向影响。

其他统计量

  • Omnibus, Prob(Omnibus): 检验残差的正态性。
  • Durbin-Watson: 2.274 检验残差的自相关性，接近2表示残差间无自相关。
  • Jarque-Bera (JB), Prob(JB): 另一个检验残差正态性的统计量。
  • Skew (偏度) 和 Kurtosis (峰度): 描述残差分布形态的统计量。
  • Cond. No (条件数): 13.6 评估模型的多重共线性问题，较大的值可能表示存在共线性问题。

image-20240301205458249

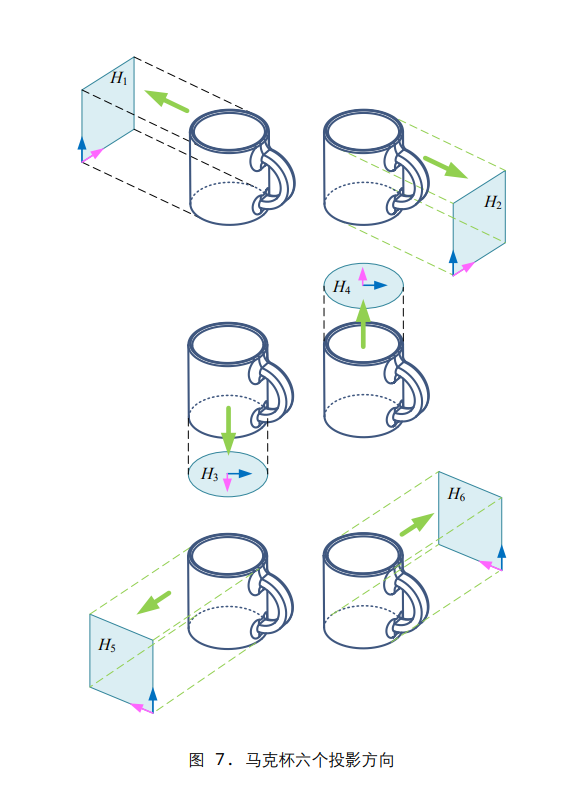
主成分分析 (principal component analysis, PCA)数据降维主成分分析将原始多维数据投影到一个新的正交坐标系，将原始数据中的最大方差 成分提取出来

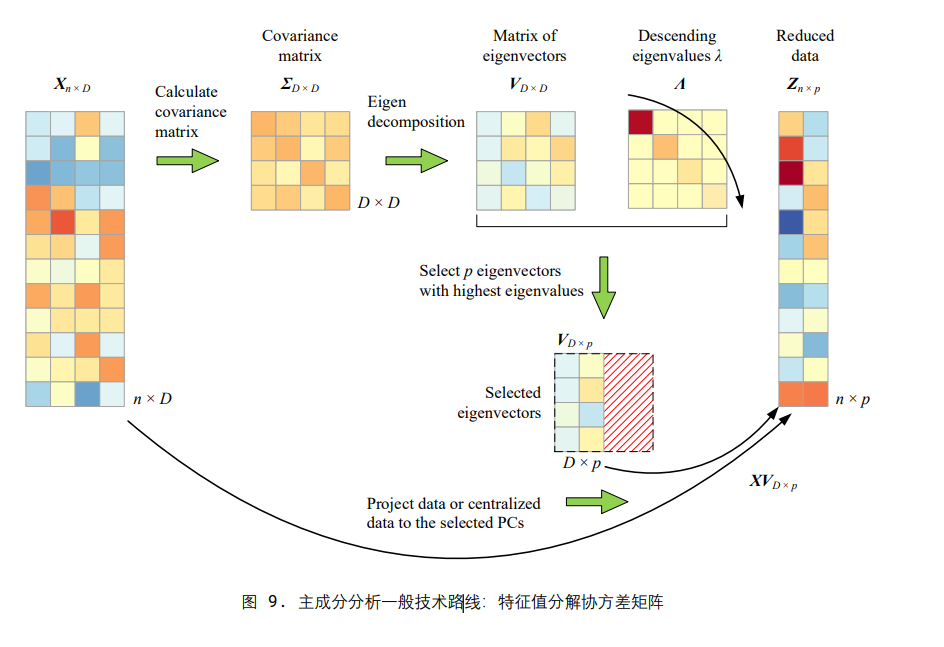
image-20240301205753408

image-20240301205800988

  1. 标准化数据：首先，通常需要对原始数据进行标准化处理，确保每个维度的均值为0，方差为1。这是因为PCA对数据的尺度非常敏感。
  2. 计算协方差矩阵：接着，计算数据的协方差矩阵。协方差矩阵能够揭示数据各维度之间的相关性。
  3. 计算特征值和特征向量：然后，计算协方差矩阵的特征值和对应的特征向量。特征向量表示数据中方差最大的方向，而特征值表示这个方向的方差大小。
  4. 选择主成分：根据特征值的大小，选择前N个最大的特征值对应的特征向量作为主成分。这些主成分是新坐标系的基，它们捕获了数据中最重要的变异性。
  5. 转换到新坐标系：最后，将原始数据投影到这些主成分上，从而实现降维。
  • 数据可视化：将高维数据降至2或3维，以便于可视化分析。
  • 特征提取和数据压缩：在不损失太多信息的前提下，减少数据的维度，提高计算效率。
  • 噪声过滤：去除数据中的噪声，保留最重要的信号。
  • 预处理：在机器学习和模式识别任务中，作为数据预处理步骤，提高模型性能。

特征值揭示了矩阵的某些内在属性，如矩阵的行列式和迹（矩阵对角线元素之和）都可以通过特征值来计算。在数据分析中，通过分析数据矩阵的特征值，可以了解数据的主要变化维度和变化幅度。

协方差矩阵（Covariance matrix）是一个表示变量间协方差的方阵，用于衡量变量间的线性相关性。在协方差矩阵中，对角线上的元素代表了每个变量的方差，而非对角线上的元素代表了两个变量间的协方差。

如果我们有一个数据集，其中包含多个变量，协方差矩阵就能帮助我们理解不同变量之间的关系。正的协方差值意味着变量间正相关，负的协方差值意味着变量间负相关，而接近零的协方差值则表示变量间没有线性关系。

假设原矩阵 �X 是一个数据集，其中每一行代表一个观测，每一列代表一个变量。协方差矩阵是通过原矩阵 �X 计算得到的，反映了 �X 中列（变量）之间的线性关系。协方差矩阵是对原始数据矩阵的一种总结和抽象，它捕获了数据的内在结构。

在主成分分析（PCA）中，协方差矩阵的特征值和特征向量扮演了核心角色。特征向量代表了数据变化的方向，而特征值的大小则代表了在这些方向上变化的幅度。通过分析协方差矩阵的特征值和特征向量，我们可以识别出数据中最重要的变化模式。

特征值 描述了特征向量的伸缩程度。在数据分析中，一个大的特征值意味着其对应的特征向量方向上数据的变异性大，即这个方向上数据有更多的信息量。